Extracto del libro de Ismael de la Cruz Instituciones de Análisis Técnico. Continuamos estudiando las medias móviles y cómo trabajar correctamente con ellas.
Continuamos viendo el resto de tipos de medias móviles:
Media triangular
La media móvil triangular suele utilizarse para suavizar las fluctuaciones del mercado. De esta manera, se construye en base a una doble media móvil simple que suaviza las fluctuaciones de los precios.
En realidad, se trata de una media con cierto retraso que siempre va por detrás del precio, otorgando la mayoría del peso a la parte media de los datos.
Esta media móvil triangular es muy similar a la media móvil exponencial y ponderada, pero en aquellas se les asigna mayor peso a los últimos datos, en la media simple se asigna igual importancia a todos los datos. Sin embargo, en la media móvil triangular el mayor peso se asigna a los datos centrales de la distribución.
Por tanto, con la media móvil triangular se le da mayor peso a la cotización central del periodo de tiempo escogido y va disminuyendo simétricamente la ponderación hacia los extremos del periodo.
Principalmente, este tipo de ponderación se lleva a cabo con medias de periodos reducidos, entre 5 y 25 días, entre otras razones para que las desviaciones de los extremos no vayan a provocar un mayor retraso del que ya de por sí es inherente a este tipo de media móvil.
Media Hull
La media móvil de Hull (nombre que se le debe su creador Alan Hull), presenta una peculiaridad bastante interesante, concretamente que es una media rápida y suave, con lo que permite que sea más estable a la variación de los precios que el resto de medias móviles, y de esta manera adaptarse rápidamente a los cambios de tendencia.
Se podría decir que la media de Hull intenta compensar el efecto de retraso que tienen las medias móviles tradicionales.
Generalmente esta media irá pegada al precio, adaptándose de manera más rápida a un giro o cambio de tendencia.
Dada sus características, es más apta para los analistas técnicos que trabajen sobre todo en el corto plazo.
Por tanto, la principal característica de ésta media es que trata de eliminar el retraso intrínseco propio de las medias móviles.
Imaginemos que tenemos una serie de 10 números, del 0 al 9; si tomamos un promedio simple de 10 periodos sobre la serie, el resultado es 4,5, el cual se encuentra bastante alejado del ultimo valor que es 9 , pero si aplicamos un promedio simple de periodo 5, sobre los últimos 5 valores, entonces el valor resultante es 7.
La clave es que si restamos 7-4,5= 2.5 ; si lo sumamos al valor de 7 nos queda 7+2.5=9.5; el cual está ligeramente por encima de 9 que es el último valor de la serie, pero mucho más cercano que el valor del promedio igual a 7 encontrado anteriormente.
Esto nos indica que la media móvil de Hull se adapta rápidamente a las variaciones en los precios permitiendo a la vez la estabilidad del mismo eliminando los efectos de los cambios bruscos.
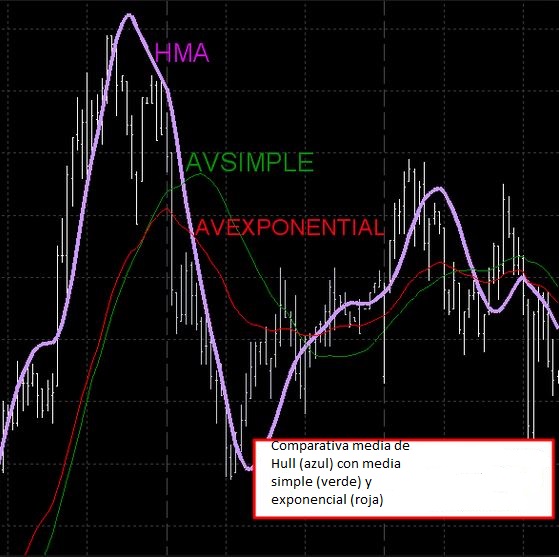
En el siguiente gráfico (cortesía de Visual Chart), pueden ver la comparativa entre la media móvil de Hull, la media móvil simple y la media móvil exponencial, siendo claramente la media de Hull la que siempre va pegada al precio y vigilándolo muy de cerca.
Otras
Existen otros tipos de medias móviles, aunque menos utilizadas por los analistas. Veamos brevemente cuáles son:
– Media móvil ajustada al volumen: estas medias móviles tienen en cuenta la evolución del precio y el volumen negociado, de forma que se le otorga mayor importancia y peso a los precios en los que se ha producido una mayor negociación.
– Medias móviles variables: en realidad se trata de medias móviles exponenciales que se encuentran ajustadas a la volatilidad de los precios.
Por tanto, es igual que una media móvil exponencial excepto que en la primera los valores de la media se ajustan automáticamente y constantemente dependiendo de la volatilidad de los datos tomados en la distribución. Así pues, cuanto mayor sea la volatilidad de la serie, mayor será el peso que se les dará a los datos más recientes.
– Medias móviles de series temporales: se trata de medias móviles que para ser calculadas se ha de acudir al tema de regresión lineal.
Ismael de la Cruz
ismaeldelacruz.es